两个三角形全等的条件(五个判定定理详解)
2023-05-27 13:56:03投稿人 : yq4qlskj围观 : 70 次0 评论
判断三角形同余有五种方法:
1.SSS，也就是并排。三条边相等的三角形是全等三角形。
2，SAS，也就是弯道。两边角相等的三角形是全等三角形。
3、ASA，也就是边角。两个角和它们的边对应于一个三角形的同余。
4，AAS，也就是边角。两个角和一个角的对边对应相等三角形的同余。
5、RHS，即直角、斜边和棱，又称HL定理(斜边和直角棱)。在一对直角三角形中，斜边和另一条直角边相等。
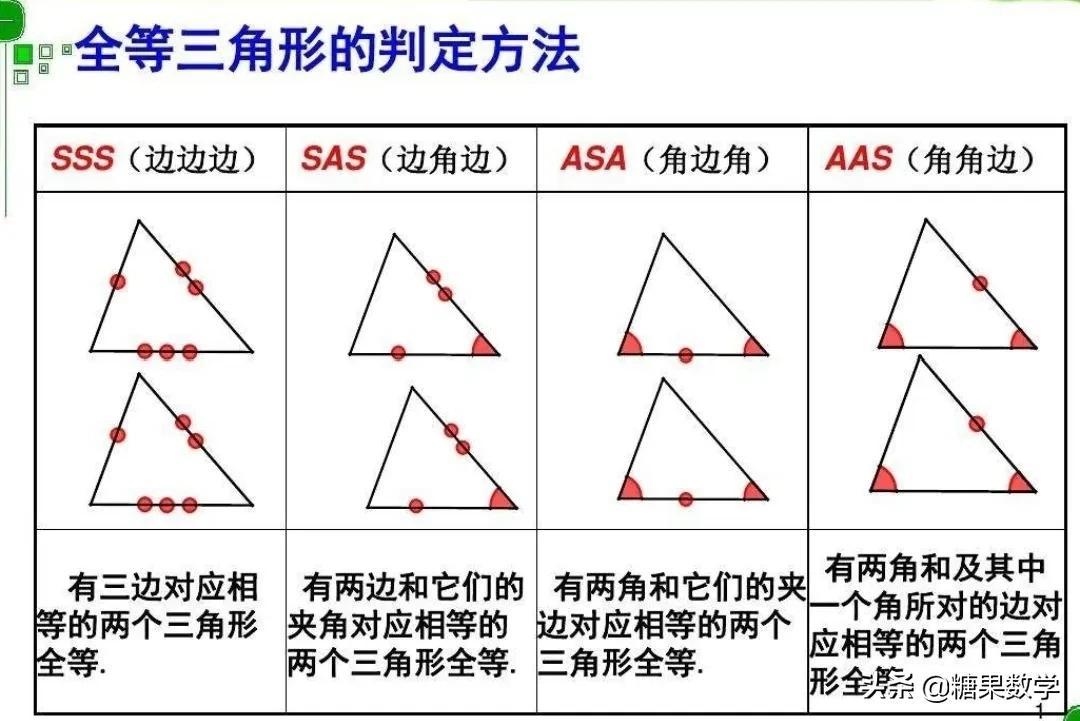
全等三角形的判断
全等三角形的本质；
1.全等三角形对应的角相等。
2.全等三角形的对应边相等。
3.能够完全重合的顶点称为对应顶点。
4.全等三角形对应边的高度相等。
全等三角形的对应角平分线相位。
等等。
6.全等三角形对应边的中线相等。
7.全等三角形的面积和周长相等。
8.全等三角形对应角的三角函数相等。
全等三角形的性质
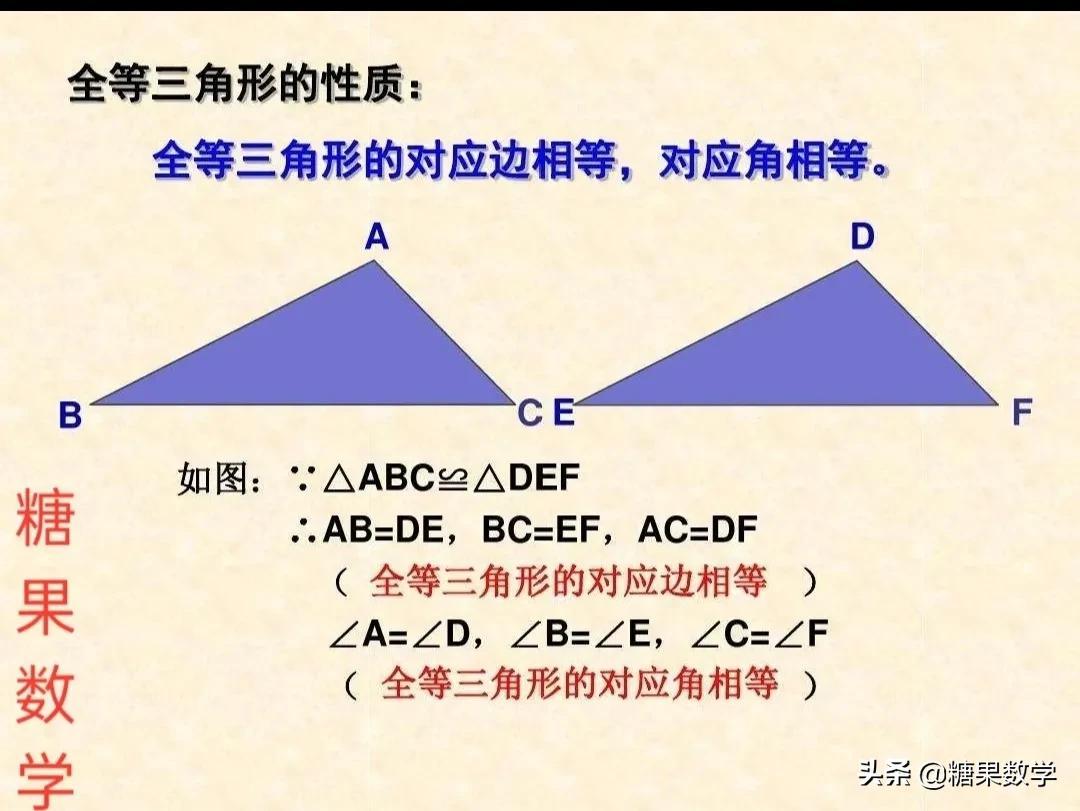
全等三角形的性质
判断三角形同余的注意事项:
三个角对应相等的两个三角形不一定全等，两条边和一条对角线对应相等的两个三角形也不一定全等。
全等三角形的应用:
1.性质中三角形的同余是一个条件，结论是对应的角和边相等。写两个三角形的同余时，对应的顶点、角和边必须按相同的顺序写，为寻找对应的边和角提供了方便。
2.当图形中出现两个以上的等边三角形时。我们应该首先考虑使用SAS来寻找全等三角形。
来源：传奇知识网，转载请注明作者或出处，尊重原创！
相关文章
黄梅时节家家雨青草池塘处处蛙的意思（黄梅时节家家雨青草池塘处处蛙的意思是什么）
本文目录一览： 1、黄梅时节家家雨,青草池塘处处蛙的意思是? 2、黄梅时节家家雨,青草池塘处处蛙.这句诗句是什么意思 3、《约客/有约》原文翻译赏析,约客/有约全诗的意思 4、黄梅时节家家雨,全诗 黄梅时节家家雨,青草池塘处处...
2024-02-22 22:29:07黄梅时节家家雨青草池塘处处蛙的意思黄梅池塘时节青草家家
发表评论