三角形重心有什么性质(三个重要性质盘点)
2023-05-27 04:53:30投稿人 : yq4qlskj围观 : 70 次0 评论
三角形的重心是三角形三条中线的交点，这是一个很特殊的点，有很多特殊的性质。一些涉及重心的问题，直接利用这些性质会事半功倍。简单总结一下吧。
1。重心到三角形顶点的距离与重心到对边中点的距离之比为2: 1。
△ In △ABC、AD、BE、CF分别是BC、AC、AB边上的中线，交点为o，则ao: od = bo: OE = co: of = 2: 1。
证明:
如图，连接EF和AD穿过G，从三角形的中线定理可知EF∨BC。又因为e是AC的中点，所以g是AD的中点。
因为△EOG∽△BOD和相似比是1: 2，我们可以计算:
Ag: go: od = 3: 1: 2，所以ao: od = 2: 1。其他原因也一样。
这个定理在一些重心需要计算边长关系的问题中相当有用。
2。三角形的重心等于由三个顶点组成的三个三角形的面积
△ In △ABC、AD、BE、CF分别为BC、AC、AB边的中线，交点为o .则sδAOB = sδBOC = sδcoa。
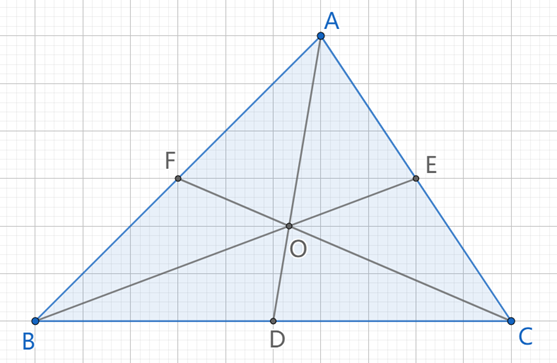
证明:S△AOB=S△BOC，其他也一样。
(计算三角形面积，基本需要做一条“高”的辅助线)
因为△AOB=△BOC有相同的底，所以它的面积比等于高长比。
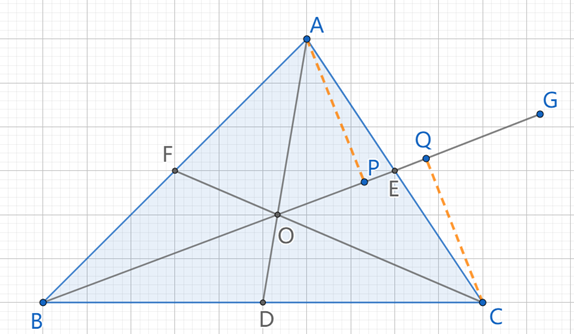
从p到a做AP⊥BE，从q到c做CQ⊥BE延长线
因为e是AC的中点，AE=CE，所以从AAS定理很容易得到△AEP≔△CEQ。
所以AP=CQ
S △ AOB: S △ BOC = AP: CQ = 1，所以S△AOB=S△BOC。
3。三角形的重心是三角形中三条边的距离乘积最大的点。
如图，O为△ABC中的一点，O到三边的距离分别为H，H，H。
验证:当O为△ABC的重心时，HHH取最大值。
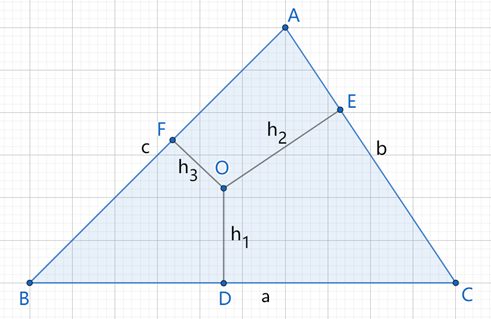
证明了设三角形的三条边为a，b，c，分别连接AO，BO，CO。
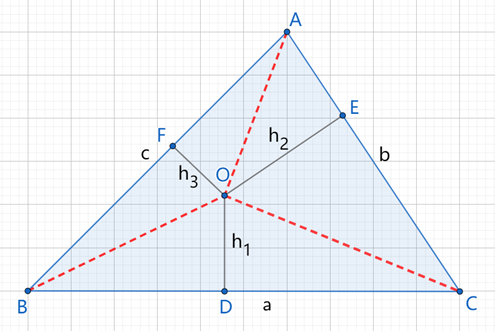
s△ABC = s△AOB+s△BOC+s△coa=1/2(a•h₁+b•h₂+c•h₃)
给定△ABC，则S△ABC为定值，三边长A、B、C也为定值。
改变的是O的位置，也就是H，H，H是变量。
如果要求HHH的最大值，那么最直观的就是利用基本不等式。
利用不等式的思路是:“量化地聚集变量。”
因为给定的量是三角形的边长和面积，所以要算出来。
HHH ≤ X (X为定值)，且必须朝向。
S △ ABC = 1/2 (ah1+bh2+CH3)。
积和的基本不等式是:几何平均数≤算术平均数
当有两个变量时，它的形式是:
当有三个变量时，它的形式是:
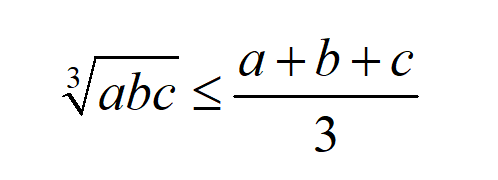
所以我们可以得到:
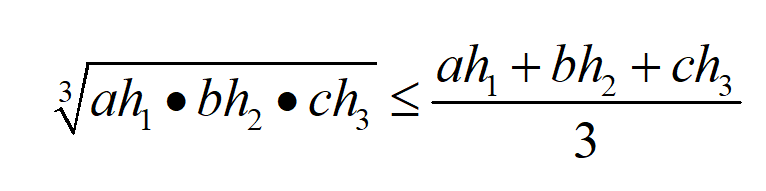
(当且仅当ah = BH = ch，等号成立，等号成立的条件极其重要。)
那么，就不需要继续计算了，只要知道AH = BH = CH时HHH是最大值就可以了。
那么此时S△AOB=S△BOC=S△COA，即O为重心。
因此，当O是△ABC的重心时，到三条边的距离的乘积最大。
来源：传奇知识网，转载请注明作者或出处，尊重原创！
相关文章
黄梅时节家家雨青草池塘处处蛙的意思（黄梅时节家家雨青草池塘处处蛙的意思是什么）
本文目录一览： 1、黄梅时节家家雨,青草池塘处处蛙的意思是? 2、黄梅时节家家雨,青草池塘处处蛙.这句诗句是什么意思 3、《约客/有约》原文翻译赏析,约客/有约全诗的意思 4、黄梅时节家家雨,全诗 黄梅时节家家雨,青草池塘处处...
2024-02-22 22:29:07黄梅时节家家雨青草池塘处处蛙的意思黄梅池塘时节青草家家
发表评论